invited

As said by its very name, the logical “square of oppositions” codifies graphically Aristotle’s logical theory of oppositions (4^th century b. C.). This concept, at the same time very abstract (for it dives into the heart of mathematical logic) and very concrete (for it evokes vividly war, conflict and all kinds of confrontations) is very important, for many reasons. Just to evoke three of them, (1) the square (and its avatars) expresses the essential properties of mathematical quantification (", $) and of logical modality ( , à); (2) perhaps more deeply, it seems to rule the functioning of “negation” (Ø) itself (negation is just a particular geometrical case of opposition), a concept as crucial – for all fields – as mysterious, as many contemporary debates, particularly in mathematical logic, show; (3) furthermore, the square of oppositions has constantly influenced the true conceptual creation in fields very distant from logic and mathematics, in so far its simplicity means a very strong (thus appealing) conceptual expressive power.

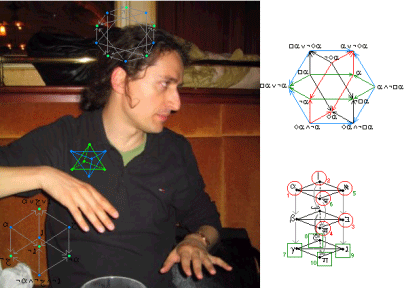
But despite this importance of the concept of opposition, it is still rather unknown that, nowadays, “opposition theory” (for short: the square) has definitively given place, in 2004, to “n-opposition theory” (an infinity of logical-geometrical, highly symmetrical, n-dimensional solids), a new rich and growing field (or zoo…) of modal logic at the intersection between abstract logic and solid n-dimensional geometry. To speak more simply (more intuitively), the logical square has given place in 1953 (thanks to Robert Blanché) to a “logical hexagon”, and in 2004, after some works of Béziau (2003) on the relations of instances of this last figure to negation, it has been proven (Moretti, Pellissier) that both the square and the hexagon, followed by a new “logical cube”, belong to a regular series of n-dimensional objects called “logical bi-simplexes of dimension n” (and the zoo goes even beyond this!).

In our present speech, after recalling, by help of many public-friendly projections of the new logical-geometrical shapes, the main trends and conceptual achievements of n-opposition theory (from where it comes, how it works, how to handle it, to where it seems to lead), we will review some of the classical pioneering new uses which were made of the old square oppositional shape outside logic (outside the zoo): for instance (but the complete list is much longer) in psychology (Piaget in cognitive science as well as Lacan in psycho-analysis), in linguistics (Greimas in semiotics as well as Austin in pragmatics) and in philosophy. From this last point of view, as a more detailed, pedagogical, example of such possible uses of the square and/or of its progeniture, we will introduce to one of such new exported models, one in pragmatics (“speech act theory”), inspired by a study of Denis Vernant about “denial” (2003), a “pragmatic hyper-cube” that we propose in order to refine a former “pragmatic hexagon”.

References